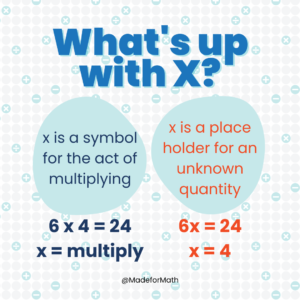Imagine this: you’re ten years old, sitting through another math lesson. Your teacher has asked you to hurry up and solve 4,358 divided by 7. You try to remember the first step…but by the time you can determine that there are six groups of 7 in 43 you have forgotten where to write the 6, and what is the next step after that?

Meanwhile, you see several classmates waving their hands in the air to share their answers with the teacher. How long have you been working on this problem? You look at the clock and quickly regret it – which one is the little hand and how do I know what it means? Then your teacher taps on your desk, “keep trying,” she demands. Okay, how many 7’s in 43 again? You quietly drop your head on your desk….

Unfortunately, this is not an uncommon classroom experience for students with dyscalculia. These students are facing so many challenges in trying to access the math instruction and then they are hurried along, which only adds to their anxiety, which further drains their working memory….and around and around we go.

There is a way to keep that child’s head off the desk, though. Check out this insightful interview with the one and only Dr. Steve Chinn. With the help of Adrianne Meldrum, (CEO of Made for Math), and Amy Anderson (one of our Multisensory Math Specialists), Dr. Chinn gives us a meaningful picture of the challenges dyscalculic learners face in the math classroom, the difficulties of teaching students with dyscalculia, and some simple ways we can make learning math more accessible for these students.

Table of Contents

Meet Dr. Steve Chinn

With decades of experience working with students with learning disabilities, a delightful sense of humor, and a charming British accent to boot, Dr. Steve Chinn is quite an amazing person. He is a teacher, an author, and a pioneer in the study of dyscalculia. He became interested in math learning disabilities when he was invited to teach at a school for dyslexic boys and noticed that dyslexia drastically impacted math learning for many of these students.

”I thought ‘this is a challenge’, and the challenge is still going 40 years later,” Chinn jokes about his first experience working with students with these learning differences. He went on to study special education at John Hopkins University and then founded his own school for dyslexic students.

Prior to teaching students with dyslexia, Chinn was a physics teacher. Since incorporating visuals into his physics lessons was a no-brainer for Chinn, he was shocked at the widespread lack of visuals used in teaching mathematics, which is so closely related to physics. This is just one of the many problems Chinn has discovered with traditional math instruction. More on this in just a bit.

Dr. Chinn has written many books detailing his research and experience with dyslexia and dyscalculia. Two of our favorites are Mathematics for Dyslexics and Dyscalculics: A Teaching Handbook and The Trouble with Maths. The summation of decades of research and experience has brought Chinn to the conclusion that we can “change the learning pattern for students” with dyscalculia and dyslexia if we simply listen.

 

“If you want to learn how to teach, listen to your students.”

Teaching students with dyscalculia and dyslexia

Dr. Chinn postures that one of the gravest mistakes educators make is to look only at what a student is doing wrong. Instead, he says, we must examine why is it wrong? For example, a child who writes the number “thirteen” as “31” is struggling with directionality. This is one of the most common obstacles for students with dyscalculia.

Another mistake we often make in teaching is to demand students work at a certain speed. Timed math fact tests, for instance, create more anxiety for students which only reduces their working memory, therefore deteriorating any opportunity to demonstrate math fact fluency. Sometimes we simply need to slow things down.

That being said, it is not enough just to… talk… slow…er. Amy Anderson jokes that we sometimes think if we say something slow enough and loud enough and repeat ourselves enough times, then somehow it will sink in for our students. Again, we must start listening to the student in order to determine the best ways to support them.

9 areas of struggle for students with dyscalculia and how to help

In his book, Mathematics for Dyslexics and Dyscalculics: A Teaching Handbook, Dr. Chinn examines some specific areas of struggle for students with dyscalculia.

1.Directional Confusion: Remember how we talked about the student who writes “thirteen” as “31”? Everyone attributes this behavior to dyslexia, but most do not stop to consider why a child’s brain would do this.

Consider for a moment the word names and matching number symbols for the first 10 numbers in the English language. Then consider the way we name and write every number after 20…twenty-one (21), twenty-two (22), thirty-five (35). It is logical that the way we say the number matches the order of the digits: the number of tens, “twenty”, followed by the number of ones. Now let’s jump back to those “teen” numbers….thirteen (13), fourteen (14), fifteen (15) – for some reason we say the number of ones first, followed by “teen” which is related to “ten”. Yet, we write the “ten” first…Kinda makes you want to bang your head on your desk, doesn’t it?

2.Sequencing Problems: Consider the ten year old trying to solve the long division problem. If you have trouble remembering the order of steps to follow to complete a math algorithm, math problems like this will be very frustrating.

3.Visual Differences: Have you ever noticed that a lot of the symbols we use in math look similar, even though they mean completely different things? Just consider the “X” used in the majority of algebraic equations to represent some unknown quantity. A dyscalculic brain will struggle to understand the difference between that “X” and the one that means multiply.

Or what about the division symbol? It appears like this ÷ when students are first introduced to the concept of division. But then it changes when students begin learning the long division algorithm. And just to further complicate things, it can also “hide” within a fraction?!

Yet another example occurs when we are teaching the value of money. Why is the dime (worth ten cents) smaller in diameter than both the nickel and penny (worth less, at five and one cent, respectively)?!

4.Spatial Awareness: I once read about a young woman with dyscalculia who said she bumped her head on a regular basis. (You can read her story here.) Dyscalculia affects a person’s ability to judge distances. So even if your student isn’t banging their head on the desk in frustration, they are likely hitting it on doors or tree branches at least occasionally.

5.Short-term Memory: Adults tend to think that if we say something over and over again, maybe a little louder, maybe even say it more slowly that “that’ll do it,” as Dr. Chinn says. But a child who struggles with short-term memory won’t grasp what you’re saying just because you change the way you say it. You need to try something different.

6.Long-term Memory: Dr. Chinn stresses that we should be “mindful of what we memorize”. Sometimes educators think everything needs to be committed to memory, but for the dyscalculic brain this may not be feasible. The multiplication (or “times”) tables are the classic example of something we fight to commit to memory, though it really isn’t necessary, and certainly isn’t fair to some.

7.Speed of Working: As if it is not determintenal enough to demand that students memorize their facts, most classrooms add on the expectation of recalling them at a certain speed. This simply is not doable for students with dyscalculia. And it quite simply is not necessary either.

8.Vocabulary: English speakers often use the same word to mean something very different. We refer to “third” place, as in a position, but then we use the same word “third” to describe 1 out of 3 pieces of a whole in fractions.

9.Language: The way we speak is confusing enough, but the way we write may be even more confusing for dyslexic and dyscalculic brains. Word problems are often a huge stumbling block for our students. When you consider that quantities in a word problem can appear in any order (not necessarily in the order needed to calculate the solution), you realize why many students misunderstand the language or simply give up. Consider the problem below:

The good news? There are so many things we can do better for students with dyscalculia. We can provide hands-on manipulatives to help them better grasp things like place value and the magnitude of numbers, we can provide nearpoint references so that students can remember the order of steps in an algorithm or the facts in a multiplication table, we can help them draw pictures to make meaning of numbers, and we can provide time and concise language to allow them better access to the math concepts.

If you are interested in learning more about this way of teaching (we call it multisensory math) click here to see a sample lesson.

3 common misconceptions of people who struggle with math

Now that you know a bit more about the areas that impact math learning for students with dyscalculia, we thought we’d share a few of the biggest misconceptions these students seem to have when it comes to math learning.

1. Zero: Dr. Chinn says, “having a symbol for nothing” causes lots of problems. This makes it especially difficult for students to understand the relationship between ten, one hundred, one thousand, and so on. They just see more zeros. Hands-on, multisensory place value instruction can help them make sense of this!

2. Algebra: “The sudden use of letters” in math equations is another big misconception. Dr. Chinn explains that students struggle to relate the letters to the numbers they represent. Again, multisensory math can help them because they are not just looking at equations on a page. Instead, we offer them concrete and pictorial representations of “unknowns” and bridge the relationship to unknowns in the form of letters.
3. Fractions: Adrianne Meldrum asserts that this is one of the greatest misconceptions of our students.  It is difficult for them to understand that a number value is smaller when the denominator gets larger. One more time, sing it from the rooftops, multisensory math makes this concept click for our students!  When they can build and manipulate parts of a whole, the magnitude of fractions becomes clear. Adrianne Meldrum asserts that this is one of the greatest misconceptions of our students. It is difficult for them to understand that a number value is smaller when the denominator gets larger. One more time, sing it from the rooftops, multisensory math makes this concept click for our students! When they can build and manipulate parts of a whole, the magnitude of fractions becomes clear.

Connect with us!

Now imagine if that ten year old student were presented with that long division problem only after having the opportunity to use manipulatives, such as base ten blocks, to touch and see the concept of dividing a number into equal groups. Imagine this child has a nearpoint reference laying on their desk to remind them of the steps needed to complete the problem and maybe a reference for the multiples of 7, too. Maybe instead of saying, “come on, hurry up!”, the teacher draws a simple picture to remind the student what division is….

If you would like to learn more about the factors that contribute to math learning difficulties, we strongly encourage you to give Dr. Chinn’s book a read! He also shares in this interview that he is working on a multiple choice version of his dyscalculia screener. And he even offers teacher trainings for educators who want to keep their students’ heads UP!

MFM Authors