Table of Contents

Perceptual Subitizing vs Conceptual Subitizing

In the realm of math education, the term subitizing might not roll off the tongue easily, but its implications are profound. Subitizing means “to see suddenly,”or the ability to recognize the number of objects in a set without counting. This is a skill inherently present in all humans, according to Dehaene’s 2003 research.

Astonishingly, even infants as young as five months exhibit a sense of automatic recognition of quantities up to approximately four, long before they can articulate the names for these quantities (Blakemore and Frith, 2005). When offered two treats in one hand and four in the other, babies will reach for the larger group.

When we arrange numbers beyond four in patterns that look like dice, it helps students to quickly recognize larger numbers. For instance, if you see a messy pile of eight things, you might have to count them or group them into smaller sets and then add those groups together to know there are eight in total. However, if you see a pattern that looks like a domino tile with eight dots, you instantly know it’s eight without counting each one. This ability to see larger numbers as made up of smaller parts is called conceptual subitizing.

Applying conceptual subitizing to math instruction connects language and numbers in the brain, making it easier to work with numbers automatically.

When students start to identify patterns within dice, they will realize they do not have to count each dot one by one to know the quantity. This link between quantity and verbal information will help their brains remember math facts. It’s especially useful for students with dyslexia because it gives them a visual way to remember, even when words are tricky for them.

The Dot Dilemma: Why We’re Ditching Dots on Numbers

We’ve observed a common practice in math education that we believe is counterproductive: the act of drawing dots directly on the numbers to assist with tying quantity to the numeral. While it may seem like a helpful visual aid, it can inadvertently hinder the development of true numeracy.

Drawing dots on numbers shifts the focus away from understanding numbers as combinations of smaller parts, which is the essence of subitizing. It can also introduce challenges, especially for students with visual or fine motor difficulties. The clutter of dots can create unnecessary visual distractions, drawing attention away from the core problem.

Furthermore, relying on dot counting as a strategy can lead to inefficiency and errors. Rather than intuitively grasping the quantity represented, students may fall back to touch counting individual dots–a time-consuming and less reliable approach.

Our recommendation? Embrace a strategy that preserves numeracy and encourages independence. Instead of drawing dots directly on numbers, encourage students to use dot patterns positioned to the side of the numbers. This approach allows for the development of true subitizing skills while offering flexibility for students to transition towards mental calculations, ultimately fostering a deeper and more enduring mathematical understanding.

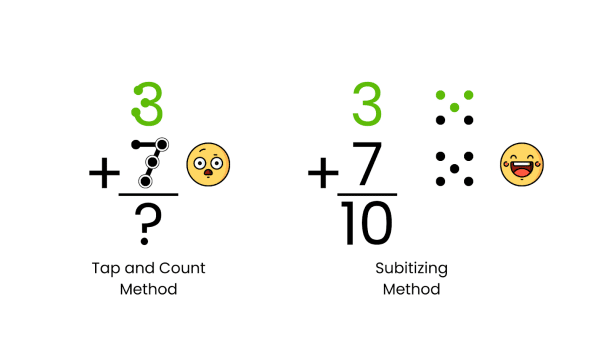
Real-Life Success Story

One of my previous students had severe dyslexia that was negatively affecting her math. She knew TouchMath but I could see how much it was slowing her down in her middle school math. I taught her the “make a ten” strategy with subitizing and she caught the concept very quickly.
 
One day we had a race. I did the column of numbers the TouchMath way and she did it the Make a Ten way. Exact same numbers. She was a competitive basketball player type, I wasn’t about to let her win. I tried super hard to do the TouchMath as fast as I could! Tap, tap, tap. And suddenly, I hear her yell out. Finished!
 
She beat me! I was half done with my column and she was completely done.
 
TouchMath was holding her back in every sense. She did not have number sense until she started learning the addends of ten with subitizing. When we only teach students to tap and count, we hinder their progress.
 
-Adrianne Meldrum

Subitizing Games

Subitizing is all about recognizing numbers instantly, and our Subitizing Playing Cards are designed to help students do just that. With various card sets featuring word and number formation, tally marks, dot patterns, and dice patterns, these cards make subitizing engaging and effective.

Grab your Subitizing Playing Cards set here.

But that’s not all! We’ve created a FREE PDF Math Games with Playing Cards Resource that perfectly complements our Subitizing Playing Cards. These games are a fantastic way to practice subitizing with your students in a fun and interactive way.

Download your FREE game resource here and start playing today!

Looking for even more subitizing resources? Explore our website for a collection of FREE Subitizing Online Games that pair seamlessly with our Math Facts to Memory book. These games are designed to reinforce math fact fluency while enhancing subitizing skills. Check them out here!

And speaking of Math Facts to Memory, if you’re on a journey to boost your students’ math fact fluency, our book is an invaluable resource. It’s filled with multisensory strategies and activities to help students build strong math fact recall on decomposing and composing within 10.

Explore Math Facts to Memory here and unlock a world of math success!

MFM Authors